| Speciální teorie relativity Autor: Neznámý Díky moc! |
Stáhněte si referát ve formátu MS Word |
Newtonova fyzika a Galileova transformace
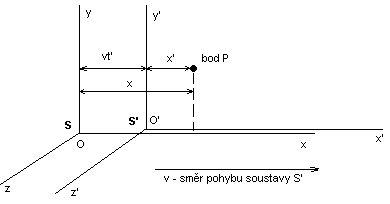
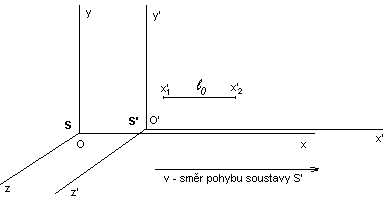
Podle prvního pohybového zákona setrvává každé těleso v klidu nebo rovnoměrném přímočarém pohybu, dokud není přinuceno působením jiného tělesa tento stav změnit. Souřadná soustava v níž pak platí pohybový zákon se nazývá inerciální soustava. Pohybuje-li se soustava souřadnic S’ (viz. obr. 1) vzhledem k jiné inerciální soustavě souřadnic S rovnoměrně přímočaře, pak soustava S’ je opět inerciální; pohybuje-li se zrychleně nebo nepřímočaře, je neinerciální.

Obrázek 1 - souřadné inerciální soustavy S a S'
Budeme nyní uvažovat dvě referenční inerciální soustavy S a S' (viz obr. 1). Osy x a x' se překrývají a budeme předpokládat, že souřadná soustava S' se bude pohybovat směrem doprava rychlostí v vzhledem k soustavě S. Pro jednoduchost umístěme počátky soustav souřadných v čase t = 0 do stejného místa. Nyní uvažujme událost, která se přihodí v bodě P o souřadnicích x', y', z' (soustavy S') v čase t. Nyní nás bude zajímat, jaké budou souřadnice této události v soustavě S. Vzhledem k tomu, že soustavy se v čase t = 0 překrývají přesně, v čase t > 0 se bude soustava nacházet ve vzdálenosti
x = x' + vt'
a ostatní souřadnice (vzhledem k tomu, že se celá souřadná soustava pohybuje podél osy x budou
y = y' z = z'
V Newtonově fyzice se předpokládá, že časy t a t' jsou totožné v obou inerciálních soustavách. Potom definujeme tzv. Galileovu transformaci:
x = x' + vt
y = y'
z = z'
t = t'
Tyto rovnice udávají souřadnice události v inerciální soustavě S, když jsou známe souřadnice v inerciální soustavě S'. Pokud známe souřadnice v soustavě S, můžeme snadno vypočítat inverzní transformací souřadnice v soustavě S':
x' = x - vt
y' = y
z' = z
t' = t
Nyní přepokládejme, že bod P představuje částici, která se pohybuje v daném směru. Složky vektoru rychlosti u'x, u'y, u'z, je potom možno vyjádřit jako:
![]()
Rychlost bodu P, tak jak je pozorována z inerciální soustavy S bude mít složky ux, uy, uz. Jejich vztah ke složkám ze soustavy S' je možno vyjádřit pomocí následující transformace:
![]()
![]()
![]()
Tyto rovnice jsou známy jako Galileova transformace.
Newtonova fyzika je založena na předpokladech, které jsou získány ze zkušenosti z každodenního života. Mezi ně patří předpoklad, že délka všech těles je stejná ve všech inerciálních soustavách, že čas ubíhá v různých inerciálních soustavách stejnou rychlostí. Tyto předpoklady jsou vyjádřeny v definici, že všechny inerciální soustavy jsou ekvivalentní.
Tyto teorie však začaly dostávat první trhliny v druhé polovině minulého století, obzvláště se studiem rychlosti světla. Teprve Albert Einstein došel k vysvětlení, které definoval ve svých dvou hlavních postulátech - principu relativity a neměnnosti rychlosti světla. Dalo by s proto říci, že obzvláště druhý postulát vyvrací Galileovu transformaci. Ukázalo se však, že Galileova transformace platí, ale pro rychlosti, které jsou mnohonásobně menší než je rychlost světla.
Lorentzova transformace
Jak vyplývá z předcházejících odstavců, bylo nezbytné odvodit nové transformace, které by splňovaly následující podmínky:
Pokud budeme opět uvažovat dvě inerciální soustavy S a S' (viz. obr. 1). Soustava S' se pohybuje ve směru osy x rychlostí v srovnatelnou s rychlostí světla. V čase t = 0 jsou počátky obou inerciálních soustav souřadných identické. Budeme proto předpokládat, že transformace je lineární a má takovouto formu:
x' = g (x - vt)
rovnice 1
x = g (x’ + vt’)
rovnice 2
kde konstanta g bude následovně určena.
Nyní, když světelný paprsek opustí společný počátek O = O’ v čase t = t’ = 0, pak v čase t > 0 urazil na ose x vzdálenost
x = ct
rovnice 3
x’ = ct
rovnice 4
Potom dosazením do těchto rovnic z rovnic 1 a 2 dostaneme
x = ct = g (ct’ + vt’) = g (c + v)t’
rovnice 5
x’ = ct’ = g (ct - vt) = g (c - v) t
rovnice 6
Další úpravou a substitucí t’ z rovnice 5 dostaneme výraz
ct = g (c + v).![]()
rovnice 7
a potom již můžeme vyjádřit z této rovnice g :
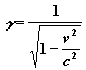
rovnice 8
Nyní nám již zbývá pouze určit vztah mezi t a t’. Toho můžeme dosáhnout zkombinováním rovnic 1 a 2.
x’ = g (x - vt) = g [g (x’ + vt)’) - vt]
pak
t = g 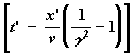
rovnice 9
. Potom s pomocí rovnice 8 vyjádříme t:
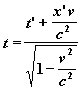
rovnice 10
Nyní můžeme celou Lorentzovu transformaci zapsat:
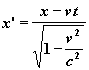
y’ = y
z’ = z
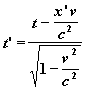
a pro transformaci v opačném směru
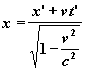 y = y’ z = z’
y = y’ z = z’
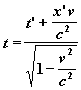
Zde stojí obzvláště za pozornost rovnice pro čas, protože zde je patrné, že čas není považován za absolutní, ale že závisí na pozici pozorovatele. Z této teorie plynou rovněž další důsledky, které budou popsány dále
Kontrakce délek
Podobně jako čas ztratil svojí absolutní hodnotu v závislosti na pozici pozorovatele, dochází k podobné situaci u délkových vzdáleností. Délka je ve speciální teorii relativita rovněž závislá na inerciální soustavě, v které se nachází pozorovatel.
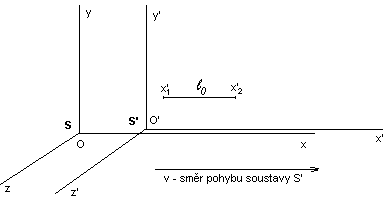
Obrázek 2
Předpokládejme opět dvě inerciální soustavy S a S’, z nichž jedna se
pohybuje rychlostí v (viz. obr. 2 - stejné umístění a pohyb, jako
v případě u obrázku 1 ). V inerciální soustavě S’ je umístěna tyč
vodorovně s osou x’ . Délka tyče v inerciální soustavě S’ je l0 ,
která je určena pomocí souřadnic ![]() koncových bodů ve stejném časovém okamžiku:
koncových bodů ve stejném časovém okamžiku:
l0 = ![]()
rovnice 11
V jakémkoliv časovém okamžiku je možné určit koncové souřadnice tyče ![]() v rámci inerciální soustavy
S pomocí Lorentzovy transformace. Délku tyče l můžeme vyjádřit v této
soustavě S jako:
v rámci inerciální soustavy
S pomocí Lorentzovy transformace. Délku tyče l můžeme vyjádřit v této
soustavě S jako:
l = ![]()
rovnice 12
K vyjádření délky tyče l v inerciální soustavě S použijeme Lorentzovu transformaci a tím získáme:
![]()
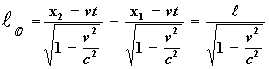
nebo pro opačný převod:
![]()
rovnice 13
Tato rovnice udává délku tělesa, jakou naměří pozorovatel, pokud se objekt kolem něj bude pohybovat rychlostí v. Je nutné podotknout, že že délková kontrakce se objevuje pouze ve směru pohybu.
Tato délková kontrakce je jedním z obecných výsledků speciální teorie relativity a platí jak pro délky objektů, tak pro vzdálenosti. Tento výsledek je možné shrnout do definice: Délka tělesa pohybujícího je kratší, než pokud by se těleso nacházelo v klidu.
Délka l0 se nazývá též skutečná délka - je to délka, kterou by naměřil pozorovatel pokud by byl vůči tělesu v klidu.
Dilatace času
Einsteinova speciální teorie relativity rovněž předpověděla, že čas ubíhá rozdílnou rychlosti v různě se pohybujících inerciálních soustavách.
Předpokládejme, že máme zdroj světla v inerciální soustavě S’, která se pohybuje rychlostí v blízké rychlosti světla (viz. obr. 3)
Obrázek 3
Souřadnice světla jsou v inerciální soustavě S’: [x', y', z']
Nyní nás bude zajímat interval D t’ - časový rozdíl
mezi dvěma událostmi, které se odehrají v soustavě S’ (například čas mezi
dvěma zablesknutími žárovky v soustavě S’). První událost se odehraje
v čase ![]() a druhá v čase
a druhá v čase ![]() a proto můžeme tento rozdíl vyjádřit jako
a proto můžeme tento rozdíl vyjádřit jako
![]()
rovnice 14
Pokud budeme chtít zjistit D t mezi dvěma záblesky tak, jak by ji změřil pozorovatel v inerciální soustavě S, musíme opět použít Lorentzovu transformaci. Časový úsek v inerciální soustavě S
![]()
rovnice 15
proto upravíme pomocí Lorentzovy transformace na a z rovnic 14 a 15 dostaneme:
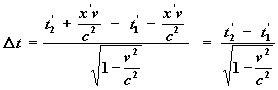
nebo vyjádřeno v zjednodušené formě:
![]()
rovnice 16
Jelikož vztah ![]() je vždy menší
než 1, je zřejmé, že platí tato nerovnost
je vždy menší
než 1, je zřejmé, že platí tato nerovnost
![]()
rovnice 17
Tato rovnice vyjadřuje, že pro pozorovatele v nepohybující se inerciální soustavě (S) se časový úsek mezi dvěma událostmi zdá delší, než stejný úsek pro pozorovatele, který se nachází v inerciální soustavě, která se pohybuje (S’). Tento výsledek plynoucí ze speciální teorie relativity se nazývá dilatace času. Obecně se dá říct, že pohybující se hodiny jdou pomaleji. Tento efekt (jak je zřejmé z rovnice 16) je však patrný teprve, pokud se hodnota rychlosti v přiblíží rychlosti světla, jinak je tento efekt zanedbatelný. Toto platí rovněž pro ostatní rovnice (kontrakce délek...)
Dilatace času patří snad právě k těm nejhůře pochopitelným (s ohledem na naší lidskou zkušenost) částem speciální teorie relativity. Patří rovněž k velice těžko prokazatelným, protože není v lidských schopnostech sestrojit objekt, který byl schopen se pohybovat rychlostí blízkou rychlosti světla. Naštěstí jsme schopni sestrojit velice přesné atomové hodiny, které jsou schopné tuto dilataci zaznamenat i při nižších rychlostech (nižších vzhledem k rychlosti světla).
Hmotnost, hybnost a energie ve speciální teorii relativity
Podle klasické Newtonovské fyziky platí, že pokud působíme na těleso konstatní silou, těleso je touto silou neustále urychlováno. Podle druhého Newtonova zákona by takový objekt měl být schopen přesáhnout dokonce rychlost světla. Toto je však v rozporu s Einsteinovým tvrzením o rychlosti světla jako maximální dosažitelné hodnoty. Proto, aby toto vyhovovalo i relativistickému pojetí, je nutno druhý Newtonův zákon (F=ma) upravit do tvaru:
![]()
rovnice 18
kde hmotnost není již konstantní, ale je funkcí rychlosti.
Dále předpokládejme, že hybnost tělesa vyjádřená rovnicí ![]() , kde m je však funkcí rychlosti. Pomocí
Lorentzovy transformace rovněž můžeme odvodit vztah pro hmotnost s ohledem na
rychlost:
, kde m je však funkcí rychlosti. Pomocí
Lorentzovy transformace rovněž můžeme odvodit vztah pro hmotnost s ohledem na
rychlost:
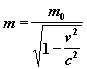
rovnice 19
kde m0 je tzv. klidová hmotnost, vzhledem k inerciální soustavě, ve které se nachází a vůči které není v pohybu.
Nyní z rovnice 19 můžeme doplnit vztah pro hybnost:
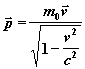
rovnice 20
Nyní zbývá určit výraz, který by vyjadřoval vztah mezi hmotností a energií.
Práce, kterou je potřeba vykonat, aby se zvýšila rychlost tělesa z 0 na v je můžeme zapsat jako:
![]()
rovnice 21
Protože d(pv) = p dv + v dp, můžeme psát:
v dp = d(pv) - p dv
rovnice 22
a potom substitucí získáme rovnici
![]()
rovnice 23
Protože integrování je přesným opakem derivování, můžeme výraz ![]() přepsat do tvaru:
přepsat do tvaru:
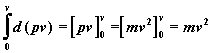
rovnice 24
kde m je funkcí v. Pak můžeme celý vztah přepsat jako
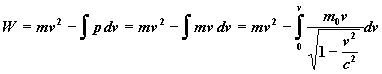
rovnice 25
Po spočítání tohoto integrálu můžeme vyjádřit konečně rovnici takto:
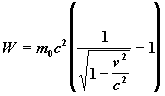
rovnice 26
Protože vykonaná práce se musí rovnat kinetické energii můžeme tuto skutečnost zapsat jako:
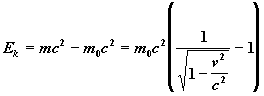
rovnice 27
kde pro rychlosti v << c výraz přechází do klasického tvaru Ek = 1/2 mv2 (Taylorův rozvoj hodnoty m = g m0v rychlosti do druhého řádu vede na klasický vztah Ek = 1/2 mv2). Výraz m0c2 se někdy též označuje jako klidová energie. Pokud tuto rovnici přepíšeme do tvaru
![]()
rovnice 28
dostává se nám nového pohledu na tuto problematiku. Výraz mc2 se nazývá celková energie E objektu, která je složená z energie v klidu plus z hodnoty kinetické energie. Celý tento poznatek můžeme zapsat do známé Einsteinovy rovnice
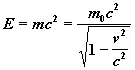
rovnice 29
a pro objekt nacházející se v klidu
E0 = m0c2
rovnice 30
Celá tato jednoduchá rovnice vyjadřuje revoluční vztah mezi hmotností a energií, kdy hmota může být přeměněna na energii a naopak. Energie se zvýší pokud se sníží hmotnost, pokud se zvýší hmotnost, musí se dodat energie. Hmotnost a energie jsou zaměnitelné veličiny.
Jednoduchou úpravou můžeme dospět k rovnici, která se nazývá Pythagorova věta o energii.
![]()
rovnice 31
Jde o užitečné vyjádření kvadrátu velikosti čtyřvektoru hybnosti. Tento vzorec je možné využít například pro fotony jejichž klidová hmotnost je nulová.
Závěr
Na konci 19. století se zdálo, že již není mnoho věcí, které by nebyly ve fyzice vysvětleny. Pak se však objevila Einsteinova teorie speciální relativity, která značně rozšířila fyzikální chápání světa a zároveň vysvětlila mnoho jevů. Teorie speciální relativity si všímá, jak se události a objekty jeví pozorovatelům v různých inerciálních soustavách. Velkým úspěchem bylo sjednocení klasické a speciální teorie relativity, kdy při nízkých rychlostech se vzorce zredukují na vzorce klasické relativity.
Speciální teorie však není aplikovatelná v neinerciálních soustavách. S tímto problémem se zabývá teorie obecné relativity. Její vysvětlení však přesahuje rámec této práce.
Shrnutí nejdůležitějších faktů
Klasická teorie relativity:
Mechanické děje dopadnou ve všech inerciálních soustavách stejně. Žádný z inerciálních systémů není nijak privilegován. Tento princip vychází z Galileovy transformace mezi dvěma souřadnicovými systémy vzájemně se pohybujícími v ose x konstantní rychlostí v.
Speciální teorie relativity
1. Mechanické i elektromagnetické děje dopadnou ve všech inerciálních systémech stejně. Žádný z inerciálních systémů není nijak privilegován.
2. Rychlost světla je ve všech inerciálních souřadnicových soustavách stejná. Princip konstantní rychlosti světla je obsažen v Maxwellových rovnicích a je podpořen celou řadou experimentů, z nichž nejznámější je Michelsonův experiment. Odpovídající transformace se nazývá Lorentzova transformace
Použitá literatura
Kapitoly ze speciální teorie relativity - Bartuška K.
Physics - Pekárek, S. Murla M.
An introduction to special relativity and its applications - Robinson. F. N. H.
Zdroje na Internetu:
http://ourworld.compuserve.com/homepages/eric_baird/sr_home.htm
http://www.desy.de/user/projects/Physics/relativity.html
http://somerset.qld.edu.au/billspages/relativity/relativity.html
http://aldebaran.feld.cvut.cz/vyuka/fyzika_2_kulhanek/relativita.html
http://math.washington.edu/~hillman/relativity.html
http://www.tri-c.cc.oh.us/METRO/Faculty/Gram/web/rel-spec.htm